Asymptotes
Asymptotes
Definition:
When a line and a curve is close to each other but never intersect or cross to each other up to infinity is called asymptotes.
There are two kind of Asymptote one is rectangular and another is called oblique asymptote.
Rectangular asymptote:
if an asymptote is parallel to x or y axis is called Rectangular asymptote. if its parallel to x axis is called horizonal asymptote and if its parallel to y axis is called vertical asymptote.
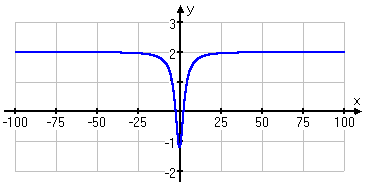
y=f(x)→Horizonal asymptote
y=2 which is horizonal asymptote
Oblique Asymptote:
if an asymptote is not parallel to x or y axis is called Oblique asymptote. Oblique asymptote is polynomial means which has positive integer exponents and don't have any friction exponent.
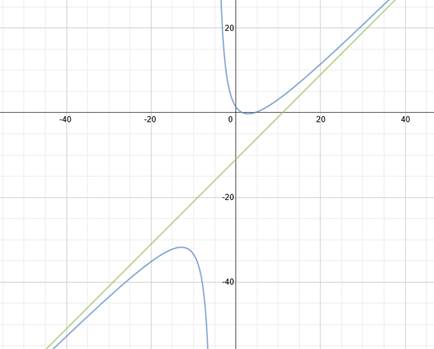
Oblique asymptote
Definition:
When a line and a curve is close to each other but never intersect or cross to each other up to infinity is called asymptotes.
Rectangular asymptote:
if an asymptote is parallel to x or y axis is called Rectangular asymptote. if its parallel to x axis is called horizonal asymptote and if its parallel to y axis is called vertical asymptote.
y=f(x)→Horizonal asymptote
y=2 which is horizonal asymptote
Oblique Asymptote:
if an asymptote is not parallel to x or y axis is called Oblique asymptote. Oblique asymptote is polynomial means which has positive integer exponents and don't have any friction exponent.
Oblique asymptote
Find Rectangular Asymptote:
- To find an asymptote parallel to x-axis equate to zero the coefficient of highest power of x in the equation of the curve.
• To find an asymptote parallel to y-axis equate to zero the coefficient of highest
power of y in the equation of the curve.
Ex:
4𝑥^2 + 9𝑦^2 = 𝑥^2𝑦^2
In this equation x and y has highest exponent 2. so we have to find out the coefficient of x^2 and y^2.
so,
4𝑥^2 + 9𝑦^2 - 𝑥^2𝑦^2 =0
=> x(4-y^2)+9y^2=0
Let coefficient = 0
(4-y^2)=0
y=+2,-2.
Its equal to x axis so we can say its horizonal asymptote.
Again,
4𝑥^2 + 9𝑦^2 - 𝑥^2𝑦^2 =0
=> y(9-^x2)+4x^2=0
Let coefficient = 0
(9-x^2)=0
x=+3,-3.
Oblique Asymptote :
Let the equation of the curve be
𝜙𝑛(𝑥, 𝑦) + 𝜙𝑛−1(𝑥, 𝑦) +……….+𝜙1 (𝑥, 𝑦) + 𝑘𝑘= 0 − (1)
where 𝜙𝑛 (𝑥, 𝑦) denotes the term of highest degree of the curve.
Step-1 Put x = 1, y = m in 𝜙𝑛(x, y), ϕn−1 (x, y), ……,𝜙𝜙1 (𝑥𝑥, 𝑦𝑦)
Step-2 Find all the real roots of 𝜙𝜙𝑛𝑛(m) = 0
Step-3 If m is a non-repeated root, then corresponding value of c is given by
c 𝜙𝑛(m) + 𝜙n−1 (m) = 0, (𝜙𝑛(m) ≠ 0)
If 𝜙𝑛(m) = 0 then there is no asymptote to the curve corresponding to this value of m.
Step-4 If m is a repeated root occurring twice, then the two values of c are given by c^2/2! *𝜙"𝑛(m) +c/1!*𝜙𝑛−1(m) + 𝜙𝑛−2 (m) = 0 (𝜙′′n (m) ≠ 0)
Step-5 The asymptote of the curve is y = m x + c
Example:
Example:
𝑥^3– 𝑥^2𝑦 – 𝑥𝑦^2 + 𝑦^3 + 2𝑥^2 – 4𝑦^2 + 2𝑥y + 𝑥 + 𝑦 + 1 = 0
Solution: In the curve the highest degree term of x is 𝑥𝑥3 and its coefficient is 1.Equating
it to 0 we get 1= 0 which is absurd, thus the curve has no asymptote parallel to x – axis.
Also the coefficient of highest degree term in y is 1, thus the curve has no
asymptote parallel to y-axis.
Now finding oblique asymptote
Here 𝜙3 (x, y) = 𝑥^3 – 𝑥^2𝑦 + 𝑦^3– 𝑥𝑦^2
𝜙2 (x, y) = 2𝑥^2 – 4𝑦^2 + 2𝑥y
𝜙1 (x, y) = 𝑥+ 𝑦
Let the asymptote be given by 𝑦 = x𝑚 + 𝑐
Step-1Putting x = 1 & y = m in ,
𝜙3 (x, y), 𝜙2 (x, y), 𝜙1 (x, y)
𝜙3 (m) = 𝑚3 – 𝑚^2 – 𝑚 + 1
𝜙2 (m) = 2 – 4𝑚^2 + 2𝑚
and 𝜙1 (m) = 1 + m
Step-2 The values of m are obtained by solving
𝜙3 (m) = 0
∴ 𝑚^3 – 𝑚^2 – 𝑚 + 1 = 0
⇒ (𝑚^2– 1) (𝑚 − 1) = 0
⇒ m = 1, 1,– 1↚ non repeated root
↜repeated root.
Here , m = –1 is a non repeated root & m = 1 is a repeated root.
For m = – 1 (non-repeated root),the corresponding value of c is given by
c𝜙3(m) + 𝜙2 (m) = 0
Now 𝜙3 (m) = 𝑚3 – 𝑚2 – 𝑚 + 1
⇒ 𝜙′3 = 3𝑚^2 – 2𝑚 – 1
∴ 𝑐(3𝑚^2 – 2𝑚 – 1) + (2 + 2𝑚 – 4𝑚^2) = 0
⇒ 𝑐=4𝑚^2 – 2𝑚 – 2/3𝑚^2 – 2𝑚 – 1 {m=(-1)}
=> C=4/4
=>C=1
Thus for 𝑚𝑚 = – 1, c= 1
Now the asymptote is 𝑦 = x𝑚 + 𝑐
i.e. 𝑦 = −𝑥 + 1 or 𝑥 + 𝑦 = 1
Step-4 For m = 1 (repeated root), the value of c is given by
c^2/2! *𝜙"𝑛(m) +c/1!*𝜙𝑛−1(m) + 𝜙𝑛−2 (m) = 0 (𝜙′′n (m) ≠ 0)
Now 𝜙'(m) = 3𝑚^2 – 2𝑚 – 1
⇒ 𝜙'' (m) = 6m − 2
𝜙2 (m) = 2 + 2𝑚𝑚 – 4𝑚𝑚2
⇒ 𝜙2'(m) = 2 − 8m
=>𝜙1 (m) = 1 + m
Putting these values in (2) we get c/2(6𝑚– 2) + 𝑐/1(-8𝑚- )+ 1 + 𝑚 = 0
𝐹or 𝑚= 1
C/2 (4) + 𝑐 (– 6) + 2 = 0
⇒ 2C^2– 6𝑐 + 2 = 0
=>c^2-3+2=0
⇒ 𝑐=3 ± √5/2 =3+ √5/2 ,3 – √5/2
For m = 1, c=
3+ √5/2 ,
∴ the asymptote is y=mx + c i.e. 𝑦 = 𝑥 +
3+ √5/2
⇒ 2𝑦= 2𝑥 + (3 + √5 )
For m = 1, c=
3–√5/2
∴ the asymptote is 2 y = 2x + (3 – √5)
∴ Three asymptotes of the given curve is
𝑥 + 𝑦 = 1,
2(𝑦– 𝑥) = 3 + √5 ,
2(𝑦– 𝑥) = 3 – √5






than you so much
ReplyDelete